7447. Обрезка строки

Дана строка s. Разрешается выбрать любые два одинаковых соседних символа и удалить их из строки. Эту операцию можно повторять, пока возможно.

Перед началом выполнения этой операции допускается удалить из строки произвольное количество символов.

Определите минимальное количество символов, которые необходимо удалить заранее, чтобы затем, применяя разрешённую операцию, получить пустую строку.

Вход. Одна строка s (1 ≤ |s| ≤ 100).

Выход. Выведите минимальное количество символов, которые следует удалить заранее.

Пример входа	Пример выхода
abacdeec	2

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть dp[l][r] = f(l, r) – минимальное количество символов, которые необходимо удалить из подстроки s_l … s_r, чтобы затем, выполняя разрешённые операции (удаление двух одинаковых соседних символов), получить пустую строку. Тогда:

· f(l, r) = 0, если l > r;

· f(l, l) = 1, так как единственный символ нужно удалить заранее;

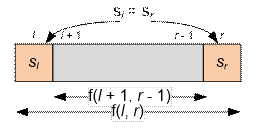
· f(l, r) = f(l + 1, r – 1), если s[l] = s[r]. В этом случае сначала удаляется внутренняя часть подстроки, после чего крайние символы становятся соседними и могут быть удалены;

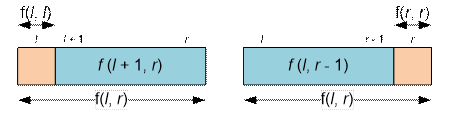
· f(l, r) = 1 + f(l + 1, r), если удаляется первый символ;

· f(l, r) = 1 + f(l, r – 1), если удаляется последний символ;

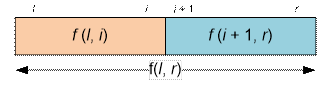
Однако оба этих случая удобно обобщить следующим образом: для решения задачи на отрезке [l; r] разобьём его на два подотрезка [l; i] и [i + 1; r] (l ≤ i < r) и выберем минимальное значение:

f(l, r) =

Например:

· удаление первого символа эквивалентно выбору i = l (f(l, l) = 1);

· удаление последнего символа эквивалентно выбору i = r – 1 (f(r, r) = 1)

Ответом на задачу будет dp[0][n – 1] = f(0, n – 1), где n – длина входной строки.

Пример

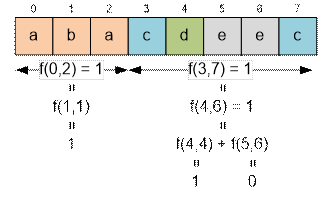
Рассмотрим пример, приведенный в условии. Имеем:

f(0, 7) = f(0, 2) + f(3, 7) = 1 + 1 = 2

Реализация алгоритма

Объявим константы и массив.

#define MAX 101

#define INF 0x3F3F3F3F

int dp[MAX][MAX];

Функция f решает задачу на отрезке [l; r].

int f(int l, int r)

{

if (l > r) return 0;

if (l == r) return 1;

if (dp[l][r] != INF) return dp[l][r];

int &res = dp[l][r];

if (s[l] == s[r])

res = min(res, f(l + 1, r - 1));

for (int i = l; i < r; i++)

res = min(res, f(l, i) + f(i + 1, r));

return res;

}

Основная часть программы. Читаем входную строку.

cin >> s;

memset(dp,0x3F,sizeof(dp));

Вычисляем и выводим ответ f(0, n – 1), где n – длина строки s.

printf("%d\n",f(0, s.size() - 1));

Java реализация

import java.util.*;

public class Main

{

static String s;

static int dp[][];

static int f(int l, int r)

{

if (l > r) return 0;

if (l == r) return 1;

if (dp[l][r] != Integer.MAX_VALUE) return dp[l][r];

int res = dp[l][r];

if (s.charAt(l) == s.charAt(r))

res = Math.min(res, f(l + 1, r - 1));

for (int i = l; i < r; i++)

res = Math.min(res, f(l, i) + f(i + 1, r));

return dp[l][r] = res;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

s = con.nextLine();

int n = s.length();

dp = new int[n][n];

for(int i = 0; i < n; i++)

for(int j = 0; j < n; j++)

dp[i][j] = Integer.MAX_VALUE;

System.out.println(f(0, n - 1));

con.close();

}

}

Python реализация

Объявим константу INF.

INF = float('inf')

Функция f(l, r) решает задачу на отрезке [l; r].

def f(l, r):

if l > r: return 0

if l == r: return 1

if dp[l][r] != INF:

return dp[l][r]

res = dp[l][r]

if s[l] == s[r]:

res = min(res, f(l + 1, r - 1))

for i in range(l, r):

res = min(res, f(l, i) + f(i + 1, r))

dp[l][r] = res

return res

Основная часть программы. Читаем входную строку s. Вычисляем ее длину n.

s = input()

n = len(s)

Инициализируем cписок dp.

dp = [[INF] * n for _ in range(n)]

Вычисляем и выводим ответ f(0, n – 1).

print(f(0, n - 1))